💻 computer science/🤔 알고리즘
📒 위상정렬
beomsic
2024. 6. 17. 15:46
💡 위상 정렬(Topological Sort)이란?
유향 그래프의 꼭짓점들(vertex)을 변의 방향을 거스르지 않도록 나열하는 것
그래프와 관련된 알고리즘 중 하나
- 방향 그래프에서 간선으로 주어진 정점 간 선후 관계를 위배하지 않도록 나열하는 정렬
❗선후 관계가 정의된 그래프 구조에서 정렬을 하는데 사용할 수 있다.
⚠️ 그래프내에 사이클이 존재하는 경우에는 올바른 위상 정렬이 존재할 수 없다.
- 선후 관계에 모순이 생기기 때문
따라서, 위상 정렬은 사이클이 존재하지 않는 방향 그래프에서만 잘 정의가 된다.
사이클이 존재하지 않는 방향 그래프 = DAG(Directed Acyclic Graph)
🧑🏻💻 구현
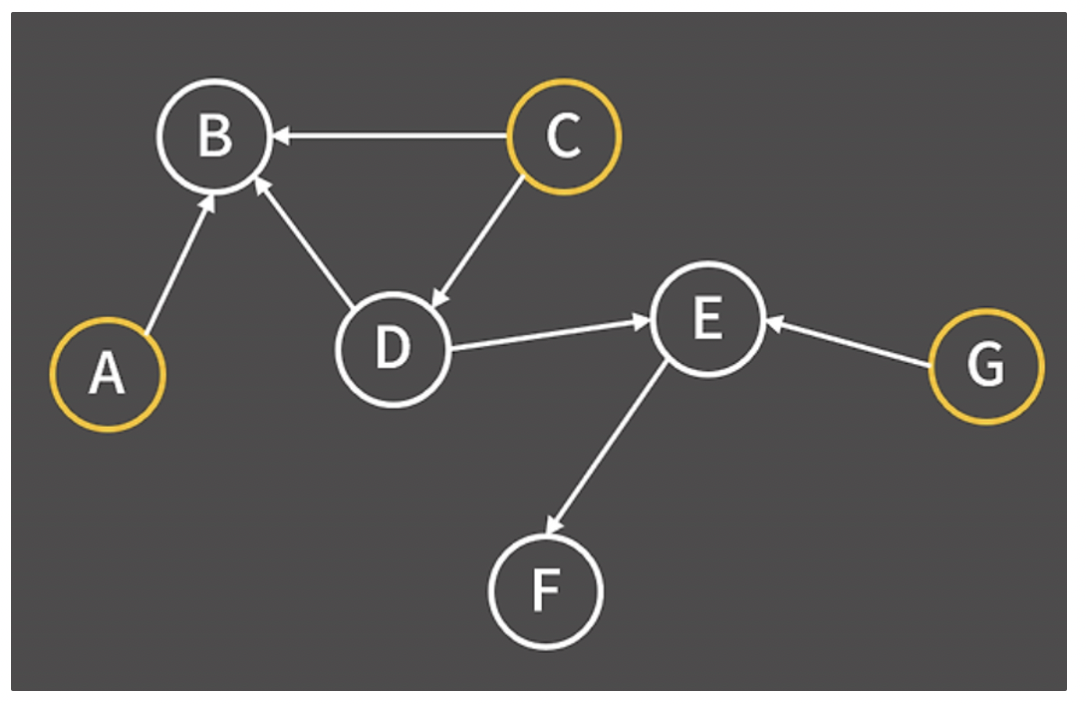
🏃 구현 순서
1️⃣ 먼저, 위상 정렬상에서 제일 앞에 오는 정점(A, C, G)로 가능한 것이 무엇인지 확인한다.
- 자기 자신에게 들어오는 간선이 없어야 한다.
2️⃣ 제일 먼저 앞에 올 수 있는 정점(A)에서 다른 정점(B)으로 나가는 간선을 생각한다.
- 이는 A가 B보다 먼저 등장해야 한다는 제약 조건을 의미
- 이 방식처럼 정점과 정점에서 뻗어나가는 간선을 모두 지운다.
3️⃣ 위와 같은 방식으로 자신에게 들어오는 간선이 없는 정점에서 2번 방법을 반복한다.
- 정점, 간선을 지워나가면서 자신에게 들어오는 간선이 없는 정점을 추가해준다.
이렇게 매 순간 들어오는 간선이 없는 정점을 제거하는 방식으로 위상 정렬을 구현한다.
🧑🏻💻 구현
1. 맨 처음 모든 간선을 읽으며 indegree 배열의 값 초기화
2. indegree 값이 0인 정점들을 Queue에 추가
3. Queue에서 정점을 꺼내 위상 정렬 결과에 추가
4. 결과에 추가된 정점으로부터 연결된 모든 정점의 indegree의 값을 1 감소시킨다.
- 만약 indegree 값이 0이 되었다면 해당 정점을 Queue에 추가
5. Queue의 값이 빌 때까지 3, 4번 과정을 반복
void topologicalSort(int[] indegree, List<List<Integer>> array) {
Queue<Integer> q = new ArrayDeque<>();
List<Integer> result = new ArrayList<>();
// indegree가 0인 정점을 큐에 삽입한다.
for(int i = 1; i <= indegree.length; i++) {
if (indegree[i] == 0) {
q.add(i);
}
}
/**
* 큐에서 원소를 꺼내 해당 원소와 간선을 제거한다.
* 만약 indegree가 0 이 된다면 큐에 넣기
* 큐가 빌 때까지 3, 4 과정을 반복한다.
*/
while (!q.isEmpty()) {
int node = q.poll();
result.add(node);
// 큐에서 원소를 꺼내 해당 원소와 간선을 제거한다.
for (int next : array.get(node)) {
indegree[next]--;
// 만약 indegree가 0 이 된다면 큐에 넣기
if (indegree[next] == 0) {
q.add(next);
}
}
}
}